"Chapter. 0 - 함수의 연속"
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

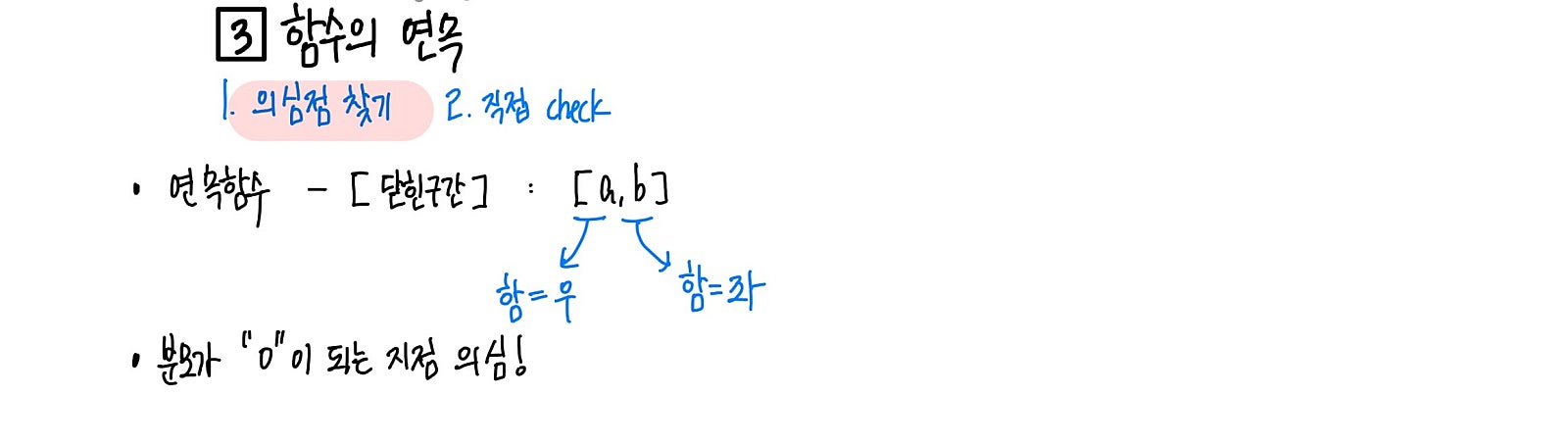
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
안녕하세요 :) 이번에는 수학적 귀납법 수열 기출문제 모음집을 배포해보려고 합니다....
-
우진희 짤 존나 많음 ㅋㅋㅋㅋ
-
전쟁은안돼ㅐ요
-
정작 실제로 좋아하게 되는 사람은 평소 얘기하던 이상형이랑 별 관련이 없음 근데 어...
-
나서기전에 방 정리 좀만 하고..
-
도시공학과분 개잘생겼다 재밌다
-
선착순4명 14
오천덕 1/19 (1)
-
진짜 레전드네 0
유일무이한 빌런이다 진짜 ㅋㅋㅋㅋ
-
심심 8
밋밋
-
네 제목은 어그로입니다 ㅈㅅ 제가 24살 신입생입니다. 원래 지방대 다니다가 군대...
-
내가왔다
-
문제집 채점 9
나자신 정신차리라는 의미임 곧글삭해야겠다 정신차려나자신
-
저는 얼굴보다 지식과 지능을 먼저 봅니다 좋아하는애 친구한테 말할때마다 걘 좀...
-
군필이면 연애 쉽다매 16
나를 속인거니..
-
벗쉬 크라크라크라 인 허 론니 헡 띵킹
-
야툰 goat 1
동아리 반박불가
-
뭔 문제가 다 저래
-
덕분에 글리젠이 ㅈㄴ 빨라졌단 거지
-
히토미나 일본 av 볼때 강간물 자주 봄 실제로 옮길 생각은 해본적 1도 없음
-
원래 4-5시에 자서 1-2시에 일어났는데 3시에 자서 11시 전에는 꼭 일어난다
-
어디이상 가야된다 보심?
-
잠도 안오는데 0
노래들으면서 일러스트나 볼까..
-
유튜버들 보면 너무 행복해보여
-
오야스미 2
네루!
-
흠
-
잘자요
-
정치성향테스트 7
tk치곤 보수가 낮게 나온거 같기도 하고..
-
뭔지는 말못해
-
젠장
-
개 웃기노 ㅋㅋㅋㅋ
-
진짜 전생같다
-
을 만들었습니다. https://kicescience.cc/strata 모바일에서도...
-
일단 많이 푼다 > 성적이 안나오면 더 많이 푼다 > 그래도 성적이 안나오면 내가...
-
예비 고3인데 아직 미적 한 번도 다 못돌았고 일단 학원 다니면서 학원교재+쎈으로...
-
꼴려하는 그 심리가 ㄹㅇ 이해안되네 걍 ㅈㄴ 수치스러울거같은데
-
올해는 오르비력 AC 1년 C가 뭔지는 상상에 맡기죠
-
빈티지룩 2
얘 왜케이쁨 잘어울리는 여자가 입었을 때가 걍 레전드임
-
메타 다 놓쳐서 이게 뭐냐
-
그랬죠..
-
아아아 근데 왜 아아아 그날만 아니었다면
-
수린이햄 사진 7
필요한사람있음?
-
왜클릭.
-
말 한번 안해본 사람을 좋아하는거면 이유가 무조건 외모임?? 16
경험자든 뭐든 의견좀
-
✊✊
-
좋아요 ㅋㅋ ㅇㄷㄴㅂㅌ
-
외 탈퇴함?
-
https://orbi.kr/00042748824 ㅋㅋㅋㅋㅋㅋ 인최업
-
아니 11
블로그쓰고왔는데 뭔떡밥임 그 고닉이 야추깜?


















































